2 title: “Proyecciones y sistemas de representación”
2.1 Tipos de proyecciones
2.1.1 Proyección cónica
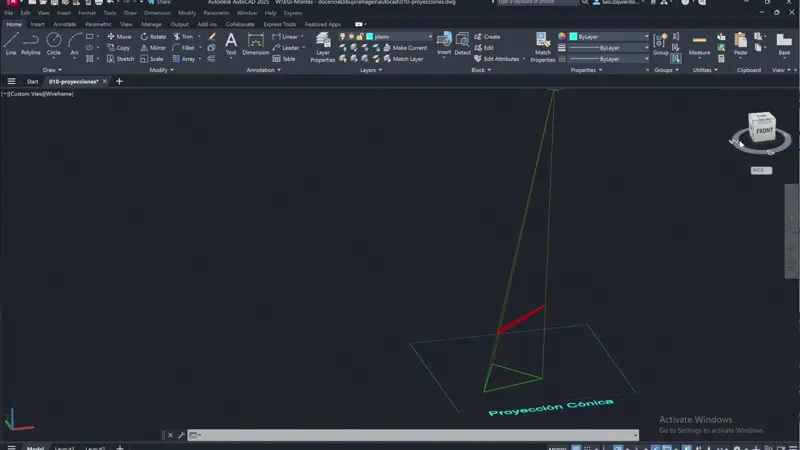
La proyección Cónica (también llamada proyección central o perspectiva) es el sistema de representación gráfico donde un haz de rectas confluyen en un punto denominado centro de proyección. Este haz de rectas proyectan el cuerpo sobre un plano auxiliar que se intersecta con dichas rectas.
2.1.2 Proyección Cilíndrica
La proyección Cilíndrica (también llamada proyección paralela) es el sistema de representación gráfico donde el centro de proyección es un punto impropio (está en el infinito).
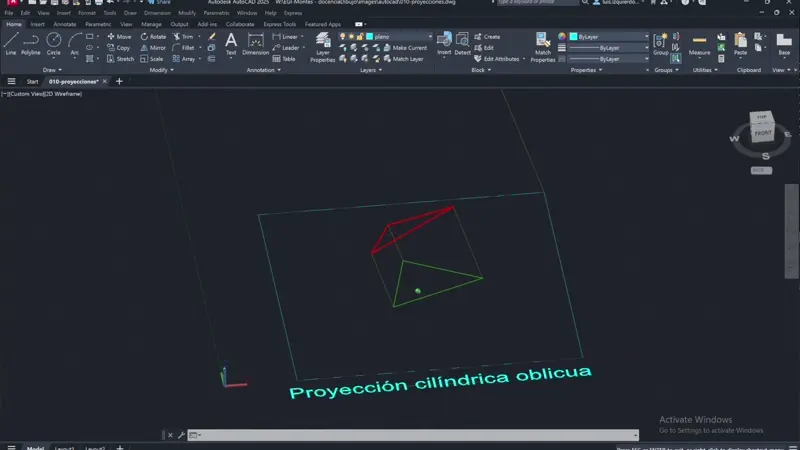
La proyección cilindrica será oblicua cuando los rayos proyectantes sean oblicuos al plano de proyección.
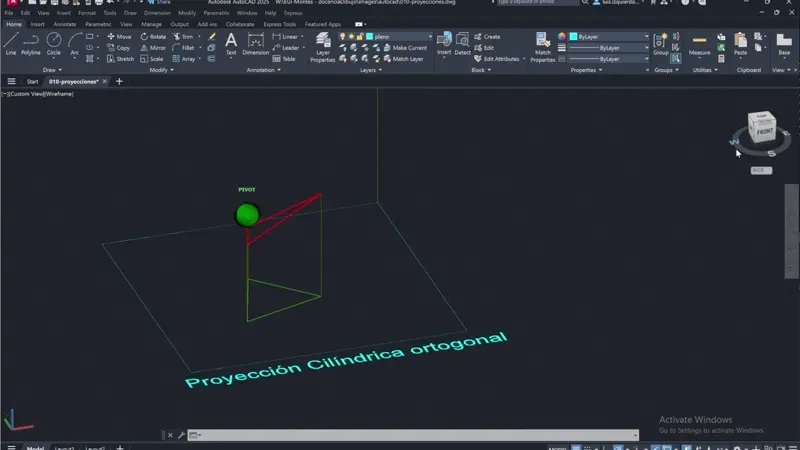
La proyección cilíndrica será orotgonal cuando los rayos proyectantes sean perpendiculares al plano de proyección.
2.2 Objeto de la Geometría Descrptiva. Sistema de Representación.
La Geometría Descriptivaes una rama de la geometría que se ocupa de la representación de objetos tridimensionales en dos dimensiones, utilizando un conjunto de métodos matemáticos y gráficos. Su objetivo principal es representar formas tridimensionales en un plano bidimensional de manera que se mantengan todas las relaciones espaciales entre los elementos del objeto, permitiendo que dichas formas puedan ser reconstruidas o visualizadas tridimensionalmente a partir de sus proyecciones bidimensionales.
Los sistemas de representación de la geometría descriptiva son: * Sistema diédrico * Sistema acotado * sistema axonométrico * Sistema cónico o central
Los tres primeros utilizan una proyección plana o colíndrina, mientras que el cuarto usa una proyección cónica. A continuación damos una breve explicación de cada uno.
2.3 Sistema Diédrico
El sistema diédrico, también conocido como proyección diédrica, es un método de la geometría descriptiva que se utiliza para representar objetos tridimensionales en dos dimensiones, mediante la proyección ortogonal de sus puntos sobre dos planos perpendiculares entre sí: el plano horizontal y el plano vertical.
Conceptos Básicos del Sistema Diédrico
2.3.1 Planos de Proyección
- Plano Horizontal (PH): Es el plano sobre el cual se proyecta la vista superior del objeto.
- Plano Vertical (PV): Es el plano sobre el cual se proyecta la vista frontal del objeto.
Ambos planos son perpendiculares entre sí y se intersecan en una línea llamada línea de tierra.
2.3.2 Proyecciones Ortogonales
En el sistema diédrico, los objetos se proyectan ortogonalmente (es decir, con líneas de proyección perpendiculares a los planos) sobre ambos planos de proyección. Estas proyecciones producen dos vistas principales: * Vista Horizontal (planta): La proyección del objeto sobre el plano horizontal. * Vista Frontal (alzado): La proyección del objeto sobre el plano vertical. A veces, también se puede incluir una vista lateral (perfil), que es la proyección del objeto sobre un tercer plano perpendicular a los dos anteriores, llamado plano de perfil.
2.3.3 Línea de Tierra
Es la línea de intersección entre el plano horizontal y el plano vertical. Sirve como referencia para alinear y relacionar las proyecciones de los puntos en ambos planos.
2.3.4 Posiciones de los Puntos y sus Proyecciones
Un punto en el espacio se representa mediante dos proyecciones: una en el plano horizontal y otra en el plano vertical. La distancia de un punto al plano horizontal se refleja en la proyección vertical, y la distancia al plano vertical se refleja en la proyección horizontal.
2.3.5 Proyecciones de Rectas y Planos
Las rectas y planos en el espacio también se proyectan en los dos planos de proyección, permitiendo entender su orientación y posición en el espacio tridimensional. Las proyecciones de una recta pueden ser paralelas o inclinadas respecto a los planos, y su verdadera longitud se visualiza dependiendo de su inclinación respecto a los planos de proyección.
2.4 Sistema Acotado
El sistema acotado es un método de representación gráfica utilizado en geometría descriptiva que se centra en la proyección de puntos, líneas, y superficies en un solo plano de proyección, con la adición de cotas o alturas para describir la tercera dimensión.Este sistema es ampliamente utilizado para representar el relieve de un terreno, donde las cotas indican las elevaciones del terreno respecto a un plano base
Conceptos básicos del Sistema Acotado:
2.4.1 Plano de Proyección
Se utiliza un solo plano de proyección, que generalmente se toma como el plano horizontal. Los objetos se proyectan ortogonalmente sobre este plano, y las alturas (cotas) de los puntos, líneas o superficies se indican mediante valores numéricos.
2.4.2 Cotas (Alturas)
Las cotas son valores numéricos que indican la altura de cada punto sobre el plano de proyección. Estos valores permiten reconstruir la forma tridimensional del objeto a partir de su proyección en el plano.
2.4.3 Proyección de Puntos
Cada punto en el espacio se proyecta como un punto en el plano de proyección, acompañado de su cota. Por ejemplo, si un punto tiene una cota de 3 unidades, esto indica que el punto está 3 unidades por encima del plano de proyección.
2.4.4 Superficies y Volúmenes (curvas de nivel o isolineas)
Las superficies planas o curvadas se representan por su contorno proyectado en el plano de proyección, acompañado de cotas que indican las alturas de diferentes puntos clave en la superficie.
2.4.5 Ventajas del Sistema Acotado
- Simplicidad: Permite representar la complejidad tridimensional en un solo plano, facilitando el análisis y la interpretación.
- Eficiencia: Al utilizar un solo plano de proyección, se simplifica la representación gráfica de objetos y estructuras.
2.5 Sistema Axonométrico
El sistema axonométrico es un método de proyección gráfica utilizado en geometría descriptiva para representar objetos tridimensionales en un plano bidimensional. A diferencia de otros sistemas de proyección, el sistema axonométrico permite que los tres ejes coordenados (X, Y, Z) sean representados simultáneamente, manteniendo las relaciones proporcionales entre ellos, lo que facilita la visualización espacial de los objetos.
Conceptos básicos del Sistema Axonométrico
2.5.1 Proyección Ortogonal Oblicua
En el sistema axonométrico, el objeto tridimensional se proyecta sobre un plano en una dirección que no es perpendicular a ninguno de los ejes, lo que permite que los tres ejes (X, Y, Z) sean visibles en la representación. Esto crea una vista en la que se pueden observar las tres dimensiones de un objeto simultáneamente.
2.5.2 Tipos de Proyecciones Axonométricas
- Isométrica: Los tres ejes están inclinados en el mismo ángulo respecto al plano de proyección, generalmente 120° entre ellos, y las dimensiones a lo largo de cada eje son igualmente escaladas.
- Dimétrica: Dos de los ejes tienen la misma escala, y el tercero tiene una escala diferente. Los ángulos entre los ejes no son iguales.
- Trimétrica: Cada uno de los tres ejes tiene una escala diferente, y los ángulos entre ellos también son diferentes.
2.5.3 Escalas y Distorsión
En el sistema axonométrico, la distorsión ocurre porque las escalas a lo largo de los ejes pueden variar dependiendo del tipo de proyección (isométrica, dimétrica, trimétrica). A pesar de la distorsión, las relaciones proporcionales se mantienen dentro de cada eje, lo que permite una representación coherente del objeto.
2.5.4 Ventajas del Sistema Axonométrico
- Visualización Completa: Permite observar las tres dimensiones de un objeto en una sola vista, lo que es útil para entender la forma y estructura general del objeto.
- Proporcionalidad: Mantiene las proporciones entre las dimensiones del objeto, aunque las escalas puedan variar.
2.5.5 Proyección Isométrica
//TODO: Explicar coeficiente de reducción, poner un par de ejemplos y gráficos
2.5.6 Proyección Dimétrica
//TODO: Explicar coeficiente de reducción, poner un par de ejemplos y gráficos
2.5.7 Perspectiva caballera como caso especial de la Proyección Dimétrica
//TODO: Explicar coeficiente de reducción, poner un par de ejemplos y gráficos
2.5.8 Proyección Trimétrica
//TODO: Explicar coeficiente de reducción, poner un par de ejemplos y gráficos
2.6 Sistema cónico o central
// TODO: terminar esta parte